Review of Methods of Solving Systems of Equations Methods of Solving Systems of Equations
Solving systems of equation three means: substitution, elimination, and graphing

There are e'er 3 ways to solve a system of equations
There are iii ways to solve systems of linear equations: commutation, elimination, and graphing. Let's review the steps for each method.
Substitution
-
Become a variable by itself in 1 of the equations.
-
Take the expression yous got for the variable in step 1, and plug information technology (substitute it using parentheses) into the other equation.
-
Solve the equation in pace 2 for the remaining variable.
-
Utilize the event from stride 3 and plug information technology into the equation from step one.

Hi! I'1000 krista.
I create online courses to help you rock your math class. Read more.
Elimination
-
If necessary, rearrange both equations so that the ???x???-terms are kickoff, followed past the ???y???-terms, the equals sign, and the constant term (in that order). If an equation appears to accept not constant term, that means that the constant term is ???0???.
-
Multiply one (or both) equations by a abiding that will allow either the ???x???-terms or the ???y???-terms to cancel when the equations are added or subtracted (when their left sides and their right sides are added separately, or when their left sides and their right sides are subtracted separately).
-
Add or subtract the equations.
-
Solve for the remaining variable.
-
Plug the upshot of step 4 into 1 of the original equations and solve for the other variable.
Graphing
-
Solve for ???y??? in each equation.
-
Graph both equations on the same Cartesian coordinate system.
-
Find the signal of intersection point of the lines (the indicate where the lines cross).
Solving the aforementioned system with commutation, so with elimination, then with graphing


Accept the grade
Want to learn more most Algebra 1? I have a footstep-by-step form for that. :)
Determining which method is all-time for solving the system: exchange, elimination, or graphing
Now allow'due south look at a few examples in which we need to decide which of these three methods to use.
Case
Which method would you utilize to solve the following problem? Explicate why you picked the method that you did.
???ten=y+2???
???3y-2x=15???
The easiest mode to solve this system would be to use substitution since ???x??? is already isolated in the first equation. Whenever ane equation is already solved for a variable, substitution will be the quickest and easiest method.
Even though you're not asked to solve, these are the steps to solve the arrangement:
Substitute ???y+2??? for ???x??? in the 2d equation.
???3y-2(y+2)=xv???
Distribute the ???-two??? then combine like terms.
???3y-2y-4=15???
???y-4=15???
Add ???iv??? to both sides.
???y-four+iv=fifteen+four???
???y=xix???
Plug ???xix??? for ???y??? into the showtime equation.
???ten=y+2???
???ten=19+2???
???10=21???
The unique solution is ???(21,nineteen)???.

There are iii ways to solve systems of linear equations: substitution, emptying, and graphing.
How to solve a system using the elimination method
Example
To solve the arrangement past emptying, what would be a useful get-go step?
???x+3y=12???
???2x-y=v???
When we use elimination to solve a system, it means that we're going to get rid of (eliminate) one of the variables. So we need to exist able to add the equations, or subtract 1 from the other, and in doing so cancel either the ???x???-terms or the ???y???-terms.
Whatsoever of the post-obit options would be a useful kickoff step:
Multiply the first equation by ???-2??? or ???ii???. This would give us ???2x??? or ???-2x??? in both equations, which will cause the ???x???-terms to cancel when nosotros add or subtract.
Multiply the 2nd equation by ???three??? or ???-3???. This would give the states ???3y??? or ???-3y??? in both equations, which will cause the ???y???-terms to cancel when we add or subtract.
Divide the second equation by ???2???. This would give usa ???10??? or ???-ten??? in both equations, which will cause the ???x???-terms to cancel when we add together or subtract.
Divide the first equation by ???iii???. This would give us ???y??? or ???-y??? in both equations, which volition cause the ???y???-terms to cancel when we add or decrease.
Let's re-practise the last instance, but instead of the elimination method, utilize a graph to detect the solution.
Solving the system past graphing both equations and finding the intersection points
Example
Graph both equations to find the solution to the arrangement.
???x+3y=12???
???2x-y=v???
In order to graph these equations, allow'southward put both of them into slope-intercept form. We become
???x+3y=12???
???3y=-x+12???
???y=-\frac13x+4???
and
???2x-y=5???
???-y=-2x+5???
???y=2x-5???
The line ???y=-(1/three)10+4??? intersects the ???y???-axis at ???4???, and and then has a slope of ???-1/iii???, so its graph is
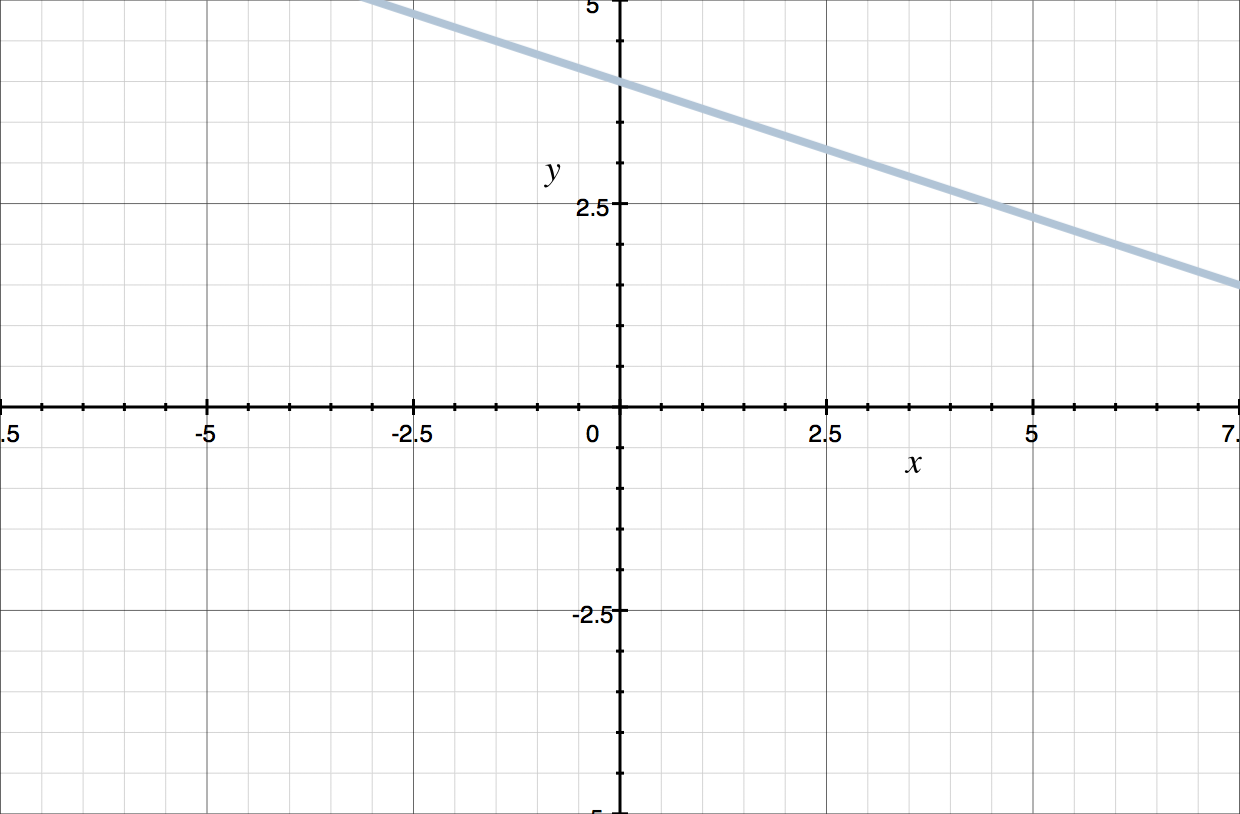
The line ???y=2x-5??? intersects the ???y???-axis at ???-5???, and and so has a slope of ???2???, then if yous add its graph to the graph of ???y=-(ane/iii)x+4???, you go
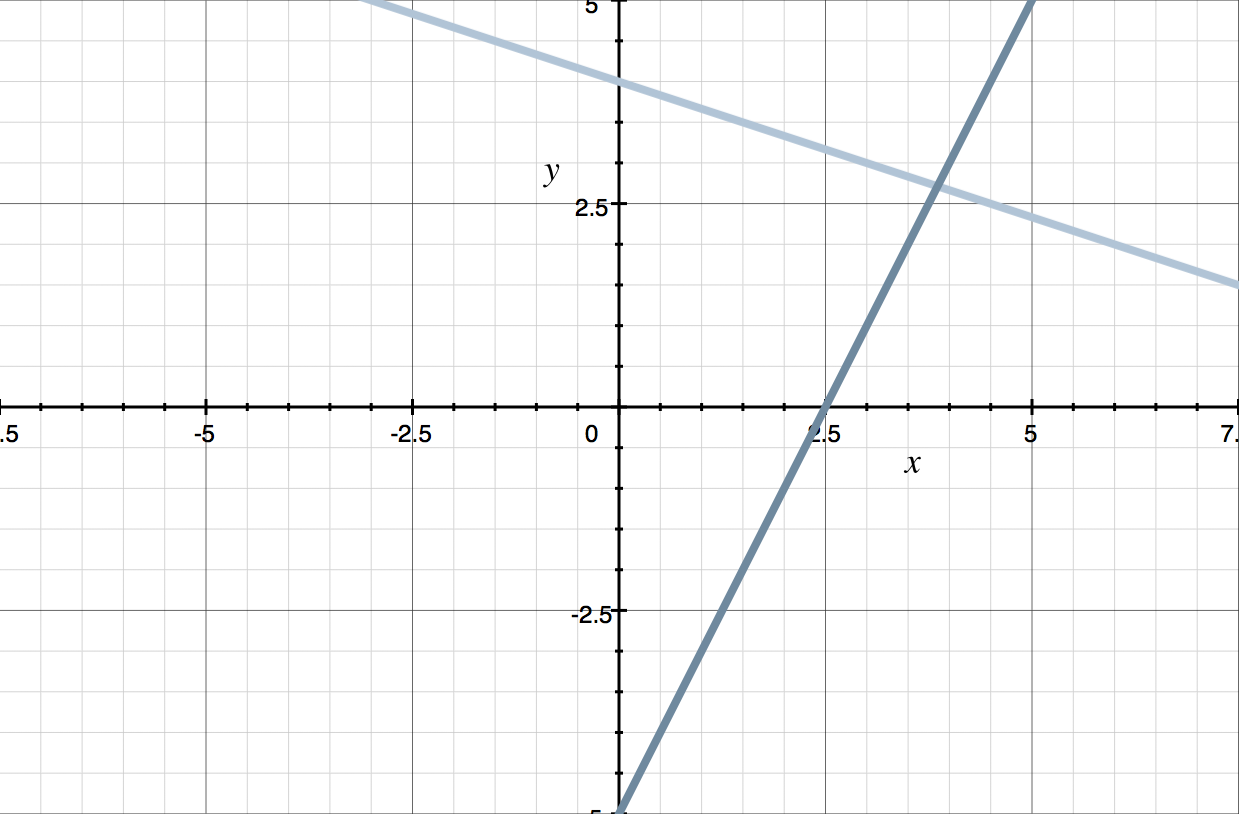
Looking at the intersection signal, it appears as though the solution is approximately ???(3.75,2.75)???. In actuality, the solution is ???(27/7,19/seven)\approx(3.86,two.71)???, and so our visual gauge of ???(3.75,two.75)??? wasn't that far off.

Get access to the complete Algebra i course
Source: https://www.kristakingmath.com/blog/solving-systems-of-equations-with-substitution-elimination-graphing
0 Response to "Review of Methods of Solving Systems of Equations Methods of Solving Systems of Equations"
Enregistrer un commentaire